In a vacuum, light travels at a velocity of c = 2.998 × 108m/sec; in more dense media, the velocity of light is lower. The index of refraction of a material, n, is defined as the ratio of the velocity of light in a vacuum to the velocity in the material, v:
n = c/v
For most calculations, the index of refraction of air can be taken as 1.0; typical indices of glasses range from 1.4 to 1.9.
Snell’s Law
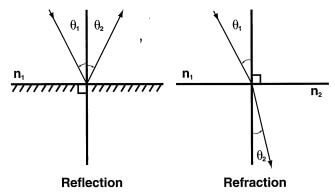
When light is incident on an interface between two materials, it can be reflected or refracted, as shown in figure below. Both situations are described quantitatively by Snell’s Law:
n1 sin θ 1 = n2 θ 2 where: n1 = index of medium 1 (incident medium)
n2 = index of medium 2
θ 1 = angle of the incident ray with respect to the surface normal
θ 2 = angle of the outgoing ray with respect to the surface normal
Reflection
In the case of reflection, both rays remain on the same side of the interface. This can be represented by setting n2 = – n1 in Snell’s Law, giving θ2 = – θ1. While reflection generally is associated with metallic surfaces such as mirrors, it also occurs at interfaces with transparent materials. With near-normal incidence on an uncoated glass interface, approximately 4% of the intensity of the incident light is reflected. The remainder refracts at the boundary and is transmitted.
Applications of Snell’s Law
Refraction
In the case of refraction, Snell’s Law states that the outgoing (refracted) ray travels in a different direction from the incident ray. For n2 > n1, the ray bends toward the surface normal. When light is incident from a medium into a less dense medium, n2 < n1, and the angle of refraction exceeds the angle of incidence, the ray bends away from the surface normal. In this case, a critical angle of incidence (θ C) occurs when θ1 = θC = sin-1 (n2/n1), which corresponds to θ2 = 90°. For θ1 > θC, no beam is transmitted; this is the condition of total internal reflection.