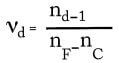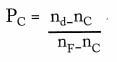The derivations of the previous equations for the object, image and focal distances assumed n1θ1 = n2θ2. However, Snell’s Law is exact; the inclusion of higher orders of the sine expansion produces slight alterations to the predictions of first-order theory. Adding the next non-zero term yields the approximation:
sin θ = θ – θ³/3!
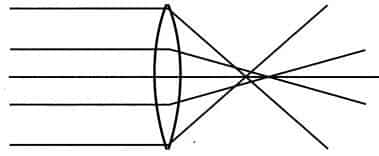
The primary third-order aberrations in monochromatic illumination are spherical, coma, astigmatism, field curvature and distortion. Spherical aberration is dependent upon focal length, aperture, shape and object position. Typically, a simple positive lens suffers from under corrected spherical aberration where off-axis rays focus closer to the lens than the paraxial rays, as shown below.
Undercorrected spherical aberration in a positive singlet
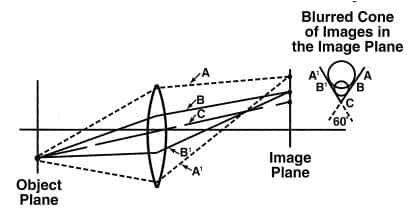
Coma is the variation in magnification of off-axis rays, caused by the refraction of light rays as they intersect various points along a spherical surface. As a result of coma, an object point is blurred into a cone-shaped image as shown in the following diagram.
Effects of coma for an off-axis object point
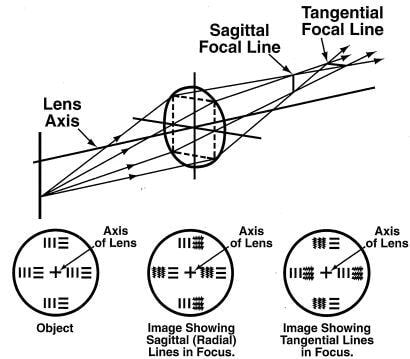
Astigmatism also degrades the image of off-axis object points. The cone of rays from a point off-axis strikes the lens asymmetrically, thus producing images at two different focal planes. The image varies from a sagittal (radial) to a tangential line, depending upon the focal position of the image plane. The resulting line images are perpendicular to each other, as illustrated below.
Effects of astigmatism
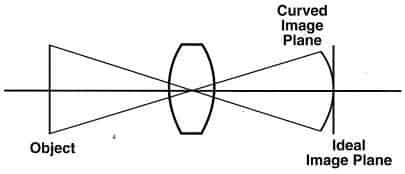
Field curvature is an image defect that causes off-axis image points to focus in different focal planes than the axial image point. Most positive lenses exhibit “inward” field curvature, that is, the image of an off-axis point falls short of the ideal image plane, causing an out-of-focus condition at the edge of the picture, when the lens is sharply focused on axis. Field curvature is inherent in every optical system, but since it is related to surface curvatures and index of refraction, it can be minimized by the lens design.
Field curvature
The final Seidel aberration is distortion. Distortion is the inability of a lens to image rectilinear objects accurately. While this deforms the image, it does not alter the focal position. The resulting imagery is shown below.
Distortion
The preceding discussion assumed monochromatic illumination. Under polychromatic illumination, the effects of dispersion must also be considered. Dispersion is the variation of the index of refraction with respect to wavelength. It is equal to nλ1 – nλ2, where λ1 and λ2 are the wavelengths for which the dispersion is expressed.
For most applications, materials are used in the visible spectrum; the n-value, or the Abbe number, expresses the relationship between the dispersion and the refracting power of the material. It is defined as:
where nd–1 is the relative refracting power and nF-nC is the measure of dispersion (nd = index of refraction at 587.6nm; nF = index of refraction at 486.1nm; nC = index of refraction at 656.3nm). Typical dispersion curves for various optical glasses are shown in figure below. This demonstrates the rate of change in the refractive indices relative to wavelength.
Dispersion Curves
It should be noted that if the secondary spectrum becomes a significant factor in performance, as in color-dependent applications, then partial dispersions become increasingly important. Partial dispersion is a measure of the rate of change in the slope of the curve relating index to wavelength and is expressed by the following relationship:
An example of this effect is the separation of white light into its spectral components by a prism.
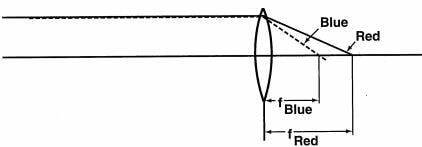
Since the index varies with wavelength, so must the angle of refraction. As a result, incident white light, made up of various wavelengths, cannot focus to a common point; chromatic aberration will occur even with an “otherwise perfect” lens. Paraxial axial color, also known as longitudinal chromatic aberration, refers to the variation of the focal length of a lens as a function of wavelength. For the same simple positive lens, shorter wavelengths form shorter focal lengths.
Longitudinal chromatic aberration
The effects of chromatic aberrations can be reduced by using a corrected doublet lens consisting of one positive and one negative element of different materials selected to minimize the total aberration. Such achromats normally are corrected for two wavelengths and exhibit reduced chromatic aberrations for intermediate wavelengths when compared to a simple lens.